Quadtree Algorithm for Implicit Curve Drawing

Implicit Curve

Background

The function which is defined as $f(x, y) = 0$ is known as implicit curve, eg. $x sin(x) + y cos(x) - 1 = 0$ is an implict curve. Similarly, the function which is in the form of $f(x, y, z) = 0$ is called implicit surface. Sometimes it is possible to convert an implicit reprentation into the explicit form, as $y - x^2 = 0$ can be written as $y = x^2$, or into parmeterized form, such as the same equation can be written as $y = t^2, x = t$ but in some cases transformation can be hard, as in $x^4 + y^4 + xy = 0$.

Explicit and parameterised curves are comparatively easier to plot than the implicit curve. To plot $y = f(x)$ which is an explict function, we have to evalute $f(x)$ at $n$ discrete location where $n$ may be horizontal resolution of the viewport, on the other hand we need to evaluate $f(x, y) = 0$ at $n^2$ different location in brute force attempt to plot implicit curves.

We can tackle the problem using two methods : A. Finding the solution of $f(x, y) = 0$ and thereafter following the curve, B. Marching cube. The first method start by solving $f(x, y) = 0$ and then exploiting gradient information to move towards the best direction. It works good in practice, but it doesn’t produce desirable result when gradient vanishes (singular points), the curve is highly twisted, or the curve is dense. The marching cube algorithm divides the viewport into small sqaures and evaluate the function at each vertex. Evaluated function value at each vertex, if function is well defined at the vetex, can either be $f(x) \le 0$, or $f(x) \gt 0$. Ignoring where $f(x_k, y_k) = 0$ at the vertex, there are sixteen possible combination of the status of four vertex. We mark each vertex of square with $sign(f(x, y))$. The square which has at least one vertex which sign differs from all other vertex or where $f(x, y) = 0$ will definitely have a curve segment if the function is continuous at every point in the square. Following figure shows different possible configuration. First and ninth squares are empty whereas eighth and sixteenth show ambiguous configuration. Marching square is a better approach than curve following however it fails handle singularties and saddle points correctly. Furtheremore, it has to evaluate $f(x, y)$ at each vertex of the square. The evaluation may be costly.

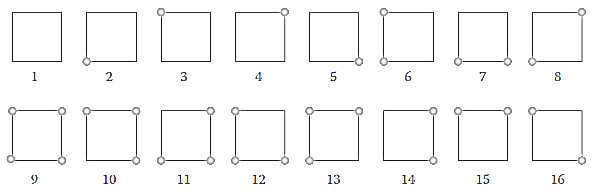Figure 1: Sixteen possible combinations: Circles represent $f(x, y) > 0$

Quadtree Algorithm for Implicit Curve

The quadtree algorithm is an extention of marching square algorithm. The space is explored recursively by the algorithm to ensure that if the curve passes through the square. The algorithm maintain two variable SEARCH_DEPTH and PLOT_DEPTH. All square cells are examined to the SEARCH_DEPTH without any function evalution. Thereafter the algorithm starts testing if a sqaure cell has a curve segment. The square cells with curve segments are explored further up toPLOT_DEPTH then the curve segment is added to the path.

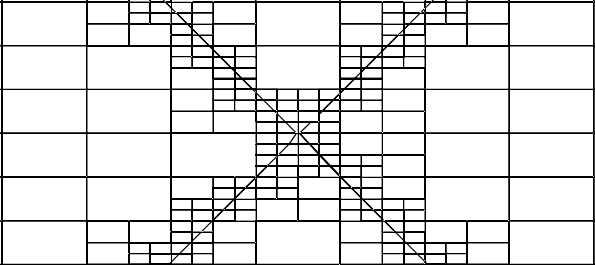Figure 2: Space exploration for |x| - |y| = 0

// this is pseudo code for quadtree algorithm
plot(x, y, dx, dy, depth) {
    if(depth < SEARCH_DEPTH) {
        dx = dx * 0.5;
        dy = dy * 0.5;
        plot(x1, y1, dx, dy, depth + 1);
        plot(x1 + dx, y1, dx, dy, depth + 1);
        plot(x1 + dx, y1 + dy, dx, dy, depth + 1);
        plot(x1, y1 + dy, dx, dy, depth + 1);
    } else {
        if(hasSegment(x1, y1, dx, dy)) {
            if(depth >= PLOT_DEPTH) {
                addSegment(x1, y1, dx, dy);
            } else {
                dx = dx * 0.5;
                dy = dy * 0.5;
                plot(x1, y1, dx, dy, depth + 1);
                plot(x1 + dx, y1, dx, dy, depth + 1);
                plot(x1 + dx, y1 + dy, dx, dy, depth + 1);
                plot(x1, y1 + dy, dx, dy, depth + 1);
            }
        }
    }
}

Digression

I implemented this algorithm for GeoGebra which supports a range of platform including desktop and web. The implemented algorithm worked fine on desktop however gui often became unresponsive when I tested the algorithm on GeoGebra Web. I tried some optimizations but they failed to work. Finally, I ran these diagonstics for java and javascript separately to discover the actual difference in performance on my 2.7 GHz, 8 GB Quad Core Dell notebook. It prohabited the algorithm from exploring the tree deeply in web view.

public class PerformanceTest {
    public static void main(String[] str) {
        long t = now();
        int k = 0;
        int z = 10000000;
        for(int i = 0; i < z; i++) {
            if(k < z) k += i;
            else k -= i;
        }
        t = now() - t;
        System.out.println("Value of k : " + k);
        System.out.println("Time taken to iterate " + z + " times: " + t);
    }
    public static long now() {
        return System.currentTimeMillis();
    }
}
// output : Time taken to execute 10000000 iteration: 20ms

time = Date.now();
k = 0;
z = 10000000;
for(i = 0; i < z; i++) {
    k++;
}
time = Date.now() - time;
console.log("Time taken to iterate " + z + " times: " + time + "ms");
// console output : Time taken to iterate 10000000 times: 15231ms

Bisection vs Linear Interpolation

Suppose the algorithm has detected a curve segment passing between two points $P(x, y)$ and $Q(x, y)$. That is, the value evaluated at point $P$ and $Q$ have opposite sign. How can we approximate the curve between $P$ and $Q$. There are two method - bisection, linear interpolation. In bisection method we take the mid-point of $P$ and $Q$. Intuitively, it is not a good method, because if the value of funtion at $P$ is more close to zero than that of function at $Q$ then it is more likely that the curve is close to point $P$.

// bisection method
Point bisection(Point p, Point q) {
    return new Point(0.5 * (p.x + p.y), 0.5 * (q.x + q.y));
}

Let’s assume that $PQ$ is parallel to x-axis and that $P = (x_1, y)$ and $Q = (x_2, y)$. Let $R = (x_r, y)$ be a point on $PQ$ where function evaluate to zero and $M = mid(P, Q)$ be the mid point of $P$ and $Q$.

The approximation at the right hand side follows because $f(x_r, y) = 0$ and higher order term have been ignored. Notice that I have dropped y term from the Taylor series expansion because of the assumption that the $PQ$ is parallel to x-axis that is y is a fixed constant. Similarly at mid point M

We can easily notice that in bisection method error is summed up and halved. We can do better using linear interpolation. For simplicity Let’s denote $f(x_1, y) = f_1, f(x_2, y) = f_2$ and $f(x_r, y) = f_r$

Here the error term in approxmation is $O({\epsilon_1}^2 - {\epsilon_2}^2)$ which is quadratic and therfore smaller than that of the bisection method for $\epsilon_1, \epsilon_2 < 1.0$

// code for linear interpolation
public Point interpolateX(Point p1, Point p2, double f1, double f2) {
    double r = f2 - f1;
    if(!Double.isFinite(r) || Double.isNan(r) || isZero(r, eps)) {
        return bisection(p1, p2);
    }
    return new Point(p2.x - f2 * (p2.x - p1.x) / r, p1.y);
}

Limitations

Quadtree algorithm performs better than marching cube algorithm, however it still suffers from certain limitations. It fails to correctly plot curve which is entirely in a single square cell, which has saddle or bifurcation point, or which intersects a square cell twice. We can handle singularities or bifurcation point by maintaining gradient information of curve, because gradient vanishes at singularities. Problem of twice intersection can be handled by communicating information among neighborhood square. However the first problem can’t be solve without exploring the tree further.

Quadtree and marching cube algorithm fails when a function changes sign but doesn’t approach to zero or a function doesn’t change sign but become zero evantually between two point. For example $\frac {1} {y-1} - 1 = 0$ is discontinous at $y = 1$, and it changes sign at $y = 1$ without having any segment there. Similarly $(x^2 + y^2 - 4)^2 = 0$ represents a circle with radius $2$ and center $(0, 0)$ however the implicit equation $(x^2 + y^2 - 4)^2$ never become negative.

Improvement in quadtree

To improve the algorithm we need to maintain gradient information and share information among neighbors. Both can increase the complexity if evaluated at each level of the tree.Therefore, combined idea of marching cube and quadtree is used. The function and its gradient is evalauted at the SEARCH_DEPTH. The gradients tend to zero near singularity. If gradients are too close to zero the algorithm mark the cell as singular. The algorithm when proceed beyond the SEARCH_DEPTH, it checks the neiborhood and mark them whenever it add a segment.

// pseudo code of modified quadtree algorithm
// grid is an nxn array
// grid status can be : 
// singular, empty, finished
grid = array(n, n);
dx = width / n;
dy = height / n;
for(i = 0; i < n; i ++) {
    for(j = 0; j < n; j ++) {
        grid[j][i] = status(x + dx * i, y + dy * j, dx, dy);
    }
}
for(k = 0; k < 8; k++) {
    for(i = 0; i < n; i++) {
        for(j = 0; j < n; j++) {
            if(grid[j][i] == FINISHED) continue;
            cell = [i, j];
            plot(x + dx * i, y + dy * j, dx, dy, SEARCH_DEPTH);
            grid[j][i] = FINISHED;
        }
    }
}
plot(x, y, dx, dy, depth) {
    if(hasSegment(x, y, dx, dy)) {
        if(depth >= PLOT_DEPTH) {
            segment = addSegment(x, y, dx, dy);
            // the function left(cell) return left side 
            // of the square, and left_cell(cell) return
            // the cell left to the current cell
            if(intersect(left(cell), segment)) {
                mark(left_cell(cell));
            }
            if(intersect(right(cell), segment)) {
                mark(right_cell(cell));
            }
            if(intersect(up(cell), segment)) {
                mark(up_cell(cell));
            }
            if(intersect(down(cell), segment)) {
                mark(down_cell(cell));
            }
        }
    }
}

Javascript implementation of quadtree algorithm

Try interactive demo here

$|xy| - 5=0$